[자료구조] 이진 탐색 트리 (Binary Search Tree)
이진 탐색 트리 (Binary Search Tree)
아래의 규칙으로 구성된 이진 트리이다.
- 왼쪽 자식 노드의 키는 부모 노드의 키보다 작다.
- 오른쪽 자식 노드의 키는 부모 노드의 키보다 크다.
- 각각의 서브 트리도 이진 탐색 트리이다.
- 중복된 키를 허용하지 않는다.
이진 탐색 트리의 특징
- 이진 탐색 트리 규칙에 의해 데이터가 정렬되어 있다.
- 이진 트리에 비해 탐색이 빠르다.
- 균형 상태 일때 : O(log n)
- 불균형 상태 일때 : O(n)
이진 탐색 트리 - 탐색
- 찾고자 하는 데이터를 루트 노드부터 비교하여 탐색한다.
- 대소 비교를 하여 찾는 데이터가 현재 노드보다 작으면 왼쪽, 크면 오른쪽 노드로 이동한다.
- 찾는 데이터가 없으면 null을 반환한다.
- 어떤 데이터를 찾더라도 최대 트리 높이 만큼의 탐색이 이루어진다.
이진 탐색 트리 - 삽입
- 루트부터 비교를 시작한다. (중복 키 발견 시 노드를 추가하지 않고 종료한다.)
- 삽입할 키가 현재 노드의 키보다 작으면 왼쪽으로 이동한다.
- 삽입할 키가 현재 노드의 키보다 크면 오른쪽으로 이동한다.
- Leaf 노드에 도달 후 키를 비교하여 작으면 왼쪽, 크면 오른쪽에 삽입한다.
이진 탐색 트리 - 삭제
(1) 삭제 대상 노드가 Leaf 노드인 경우 : 삭제 대상 노드를 그냥 삭제하면 된다.
(2) 삭제 대상 노드에 자식 노드가 하나 있는 경우 : 자식 노드를 삭제 대상 노드의 부모 노드에 연결하고 삭제 대상 노드를 삭제한다.
(3) 삭제 대상 노드에 자식 노드가 둘인 경우
- i) 삭제 대상 노드의 왼쪽 서브 트리에서 가장 큰 노드를 선택한다.
- ii) 삭제 대상 노드의 오른쪽 서브 트리에서 가장 작은 노드를 선택한다.
- i 또는 ii 에서 선택한 노드를 삭제 대상 노드 위치로 이동시킨다.
- 이동하는 과정에서 다른 자식 노드들의 링크 연결 작업을 진행한다.
- 삭제 대상 노드를 삭제한다.
균형 이진 탐색 트리 (Balanced Binary Search Tree)
모든 노드의 좌우 서브 트리 높이가 1이상 차이 나지 않는 트리이며, 노드의 삽입과 삭제가 일어날 때 균형을 유지하도록 하는 트리이다.
이진 탐색 트리는 삽입 순서에 따라 트리의 구조가 한쪽으로 치우치는 경우 즉, 편향이 발생할 수 있다.
편향된 이진탐색 트리는 하나의 branch(분기)만을 가지고 있으며, 이로 인해 트리의 높이가 크게 증가하게 된다.
이는 검색, 삽입, 삭제 연산의 성능을 저하시킬 수 있다.
이러한 경우를 방지하기 위해 균형 이진 탐색 트리를 사용한다.
AVL 트리
- 노드가 삽입, 삭제될 때 트리의 균형을 체크하고 유지하는 트리
- 각 노드의 BF를 [-1, 0, 1] 만 가지게 하여 균형을 유지한다.
- BF (Balance Factor) : 왼쪽 서브 트리 높이 - 오른쪽 서브 트리 높이
- AVL 트리 - 리밸런싱
- 균형이 깨진 경우
- BF가 ‘+2 이상’이면 왼쪽 서브 트리에 이상이 있음
- BF가 ‘-2 이’이면 오른쪽 서브 트리에 이상이 있음
- 회전 연산
- 단순 회전 - LL, RR
- 이중 회전 - LR, RL
- 균형이 깨진 경우
(1) AVL 트리 - LL (Left-Left) : 회전 1회, 오른쪽 방향으로 회전
(2) AVL 트리 - RR (Right-Right) : 회전 1회, 왼쪽 방향으로 회전
(3) AVL 트리 - LR (Left-Right) : 회전 2회, RR 회전 후 LL 회전
(4) AVL 트리 - RL (Right-Left) : 회전 2회, LL 회전 후 RR 회전
Red-Black 트리
- 조건
- 루트 노드와 리프(NIL) 노드의 색은 black
- red 색 노드의 자식은 black (double red 불가)
- 모든 리프 노드에서 루트 노드까지 가는 경로의 black 노드 수는 같다.
(1) Red-Black 트리 - 삽입 Case 1

- 부모 노드의 형제 노드가 red 일 때
- Recoloring 진행
- 삽입한 노드의 부모와 부모의 형제 노드를 black 으로 변경
- 부모의 부모 노드를 red로 변경
- 부모의 부모 노드가 root인지 double red인지에 따라 조정 진행
(2) Red-Black 트리 - 삽입 Case 2
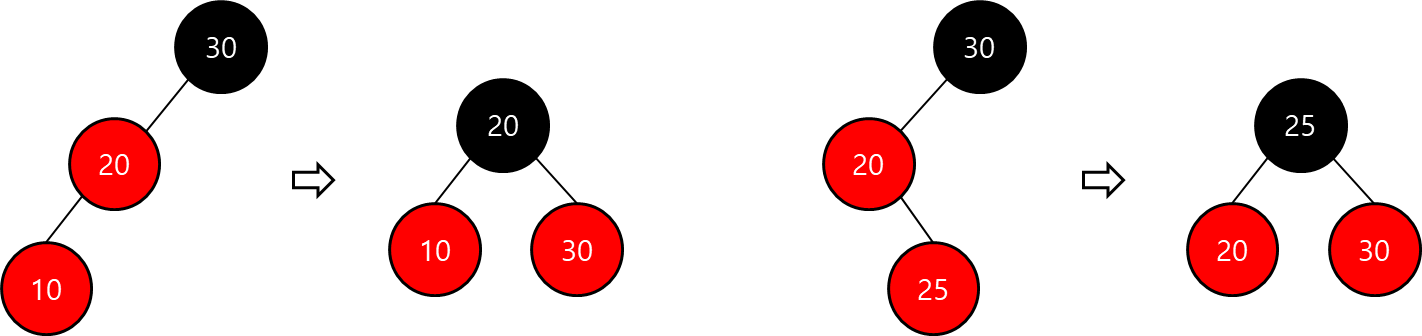
- 부모 노드의 형제 노드가 black 이거나 없을 때
- Restructuring 진행
- 조정 대상 : 삽입한 노드, 부모 노드, 부모의 부모 노드
- 조정 대상 노드들을 오름차순 정렬
- 가운데 노드를 부모 노드로 선정하고 black 으로 변경
- 나머지 두 노드를 자식 노드로 두고 red로 변경
(3) Red-Black 트리 - 삭제 기본 Case

- 삭제 대상 노드가 black 이고 그 자리에 오는 노드가 red 인 경우
- 해당 자리로 오는 red 노드를 black 으로 변경
(4) Red-Black 트리 - 삭제 이중 흑색 1 (Double Black Case 1)

- 삭제 대상 노드가 black, 그 자리에 오는 노드가 black 인 경우
- 이중 흑색 노드의 형제 노드가 black 이고, 형제의 양쪽 자식 모두 black 인 경우
- 형제 노드를 red로 변경
- 이중 흑색 노드의 검은색 1개를 부모 노드로 전달
- 부모가 루트가 아닌 이중 흑색 노드가 되면 해당 case를 반복한다.
(5) Red-Black 트리 - 삭제 이중 흑색 2 (Double Black Case 2)

- 이중 흑색 노드의 형제 노드가 red인 경우
- 형제 노드를 black으로 변경
- 부모 노드를 red로 변경
- 부모 노드를 기준으로 왼쪽으로 회전
- 그 다음 이중 흑색 case에 따라 반복 진행
(6) Red-Black 트리 - 삭제 이중 흑색 3-1 (Double Black Case 3-1)

- 이중 흑색 노드의 형제 노드가 black 이고, 오른쪽 자식이 red인 경우
- 부모 노드와 형제 노드의 오른쪽 자식 노드를 검은색으로 변경
- 부모 노드를 기준으로 왼쪽으로 회전
(7) Red-Black 트리 - 삭제 이중 흑색 3-2 (Double Black Case 3-2)

- 이중 흑색 노드의 형제 노드가 black 이고, 왼쪽 자식이 red인 경우
- 형제 노드를 red로 변경
- 형제 노드의 왼쪽 자식 노드를 검은색으로 변경
- 형제 노드를 기준으로 오른쪽으로 회전
- 이중 흑색 3-1 case 진행
AVL 트리 vs Red-Black 트리
- 알고리즘 시간 복잡도 : 둘다 O(log n)
- 균형 수준
- AVL 트리가 Red-Black 트리 보다 좀 더 엄격하게 균형 잡음
- Red-Black 트리는 색으로 구분하는 경우로 인해 회전 수가 감소
- 실 사용 시
- 트리 체계가 잡힌 후, 탐색이 많은 경우에는 AVL 트리가 유리
- 삽입, 삭제가 빈번한 경우에는 Red-Black 트리가 유리