2167번: 2차원 배열의 합 (acmicpc.net)
2167번: 2차원 배열의 합
첫째 줄에 배열의 크기 N, M(1 ≤ N, M ≤ 300)이 주어진다. 다음 N개의 줄에는 M개의 정수로 배열이 주어진다. 배열에 포함되어 있는 수는 절댓값이 10,000보다 작거나 같은 정수이다. 그 다음 줄에는
www.acmicpc.net
문제
2차원 배열이 주어졌을 때 (i, j) 위치부터 (x, y) 위치까지에 저장되어 있는 수들의 합을 구하는 프로그램을 작성하시오. 배열의 (i, j) 위치는 i행 j열을 나타낸다.
입력
첫째 줄에 배열의 크기 N, M(1 ≤ N, M ≤ 300)이 주어진다. 다음 N개의 줄에는 M개의 정수로 배열이 주어진다. 배열에 포함되어 있는 수는 절댓값이 10,000보다 작거나 같은 정수이다. 그 다음 줄에는 합을 구할 부분의 개수 K(1 ≤ K ≤ 10,000)가 주어진다. 다음 K개의 줄에는 네 개의 정수로 i, j, x, y가 주어진다(1 ≤ i ≤ x ≤ N, 1 ≤ j ≤ y ≤ M).
출력
K개의 줄에 순서대로 배열의 합을 출력한다. 배열의 합은 231-1보다 작거나 같다.
풀이
처음에는 단순하게 반복문을 통해 sum을 구했다.
통과는 했지만 시간이 너무 오래 걸려서 다이나믹 프로그래밍을 사용하여 다시 풀었다.
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class No2167_SumOfTwoDimensionArrays {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
// 배열 생성
int[][] arr = new int[N + 1][M + 1];
for (int i = 1; i <= N; i++) {
st = new StringTokenizer(br.readLine());
for (int j = 1; j <= M; j++) {
arr[i][j] = Integer.parseInt(st.nextToken());
}
}
int K = Integer.parseInt(br.readLine());
for (int k = 0; k < K; k++) {
st = new StringTokenizer(br.readLine());
int i = Integer.parseInt(st.nextToken());
int j = Integer.parseInt(st.nextToken());
int x = Integer.parseInt(st.nextToken());
int y = Integer.parseInt(st.nextToken());
int sum = 0;
// sum 구하기
for (int a = i; a <= x; a++) {
for (int b = j; b <= y; b++) {
sum += arr[a][b];
}
}
System.out.println(sum);
}
}
}배열 생성하는 부분 변경
dp[1][1] = arr[1][1]
dp[1][2] = dp[1][1] + arr[1][2]
dp[1][3] = dp[1][2] + arr[1][3]
dp[2][1] = dp[1][1] + arr[2][1]
dp[2][2] = dp[2][1] + dp[1][2] 를 한 후 dp[2][1]과 dp[1][2]에 공통으로 있는 dp[1][1]을 빼줘야 하므로
최종 식 = dp[2][1] + dp[1][2] - dp[1][1] + arr[2][2]
dp[2][3] = dp[2][2] + dp[1][3] - dp[1][2] + arr[2][3]
int[][] arr = new int[N + 1][M + 1];
int[][] dp = new int[N + 1][M + 1];
for (int i = 1; i <= N; i++) {
st = new StringTokenizer(br.readLine());
for (int j = 1; j <= M; j++) {
arr[i][j] = Integer.parseInt(st.nextToken());
dp[i][j] = dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1] + arr[i][j];
}
}sum 구하는 부분 변경
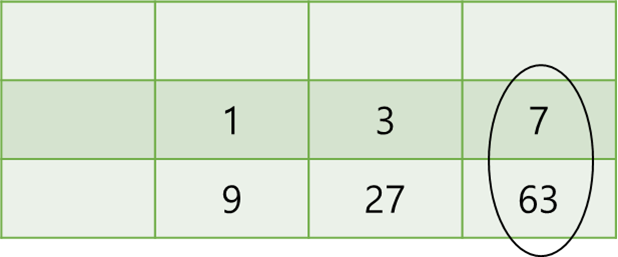
(1, 3)(2, 3) 이 주어졌을 때 합 = dp[2][3] - dp[2][2] - dp[0][3] + dp[0][2] 이다.
dp[2][2] 를 빼는 이유는 아래의 그림에서 동그라미친 부분의 합을 구해야 하기 때문에 63에 들어있는 27을 제거하기 위해서다.
그리고 dp[0][3] + dp[0][2] 부분은 지금은 영향이 없지만 n과 m이 더 커졌을 때를 생각하여 추가했다.
int sum = dp[x][y] - dp[x][j - 1] - dp[i - 1][y] + dp[i - 1][j - 1];변경 후 시간이 거의 6분의 1로 줄었다.

'백준' 카테고리의 다른 글
| [백준 2003번][Java][투 포인터] 수들의 합 2 (0) | 2023.04.03 |
|---|---|
| [백준 1254번][Java] 팰린드롬 만들기 (0) | 2023.04.03 |
| [백준 11725번][Java][Tree][DFS] 트리의 부모 찾기 (0) | 2023.03.27 |
| [백준 5613번][Java] 계산기 프로그램 (0) | 2023.03.27 |
| [백준 2830번][Java][비트연산자] 행성 X3 (0) | 2023.03.21 |